HEIDENHAIN iTNC 530 (340 420) - Příručka (Stránka 143)

HEIDENHAIN iTNC 530 117
5.4
T
rojr
o
změrná ko
rekc
e
nástr
oje
Definice normovaného vektoru
Normovaný vektor je matematická veličina, která má velikost 1 a
libovolný směr. U bloků LN potřebuje TNC až dva normované vektory
jeden pro určen směru normály plochy a jeden (volitelný) pro
určen směru orientace nástroje. Směr normály plochy je definován
složkami NX, NY a NZ. Ukazuje u stopkové a rádiusové frézky kolmo
od povrchu obrobku ke vztažnému bodu nástroje PT, u rohové frézky
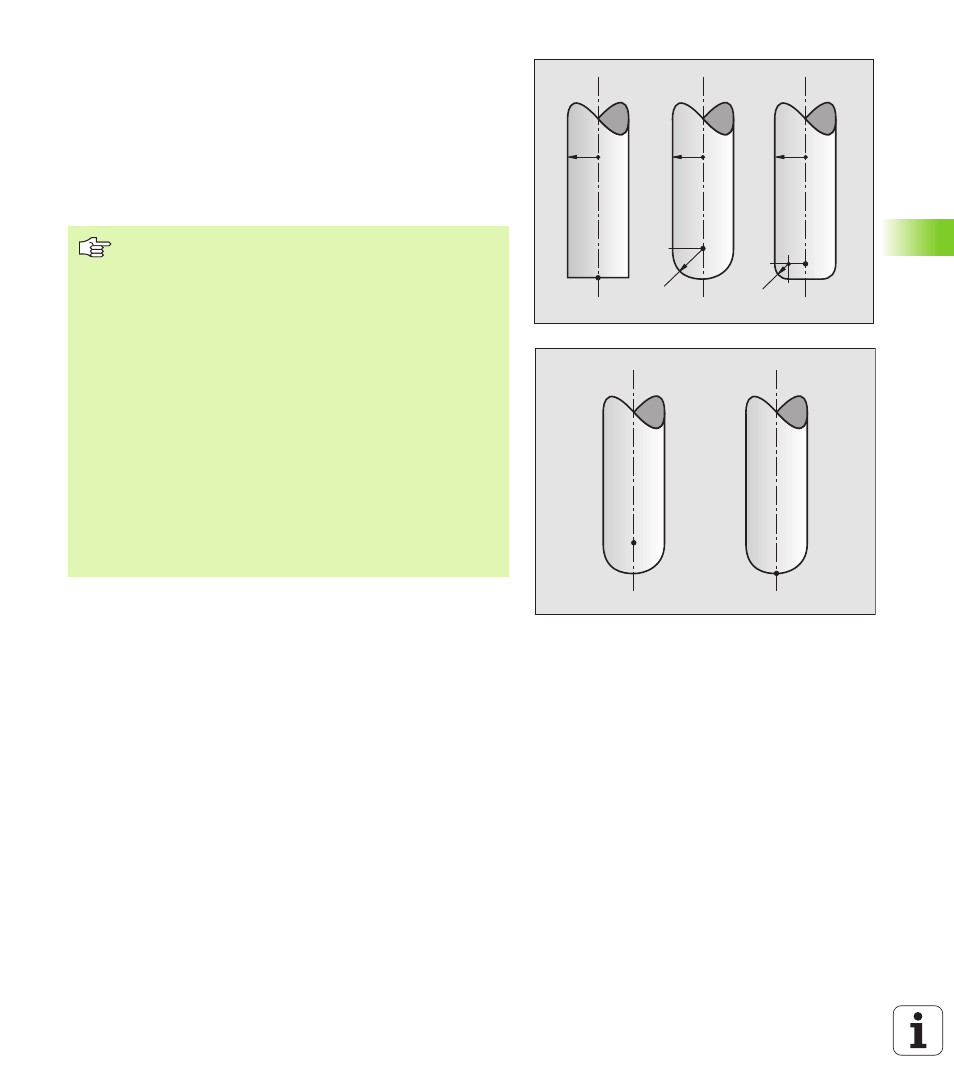
skrz PT‘ př padně PT (viz obrázek vpravo nahoře). Směr orientace
nástroje je určen složkami TX, TY a TZ.
Dovolené formy nástroje
Dovolené formy nástroje (viz obrázek vpravo nahoře) definujte do
tabulky nástrojů pomoc rádiusů nástroje R a R2:
n
Rádius nástroje R: rozměr od středu nástroje k vnějš straně
nástroje.
n
Rádius nástroje 2 R2: rádius zaoblen od špičky nástroje k vnějš
straně nástroje
Vzájemný poměr R ku R2 definuje tvar nástroje:
n R2 = 0: Stopková fréza
n R2 = R: Rádiusová frézka
n
0 < R2 < R: Fréza s rohovým rádiusem
Z těchto údajů lze také z skat souřadnice pro vztažný bod nástroje PT.
Souřadnice pro polohu X, Y, Z a pro normály plochy NX,
NY, NZ, př padně TX, TY, TZ mus m t v NC bloku stejné
pořad .
V bloku LN udávejte vždy všechny souřadnice a všechny
normály plochy, i když se hodnoty proti předchoz mu
bloku nezměnily.
3D korekce s normálami plochy je platná pro zadán
souřadnic v hlavn ch osách X, Y, Z.
Pokud vyměn te nástroj s př davkem (kladná delta
hodnota), pak TNC vyp še chybové hlášen . Chybová
hlášen můžete potlačit pomoc M funkce M107 (viz
„Předpoklady pro NC bloky s normálovými vektory
plochy a 3D korekc ”, str. 111).
TNC nevaruje chybovým hlášen m, když by byl nadm rou
nástroje poškozen obrys.
Ve strojn m parametru 7680 nadefinujete, zda CAD
systém zkorigoval délku nástroje přes střed koule P
T
nebo jižn pól koule P
SP
(viz obrázek vpravo).
P
T
R R R
R2
P
T P
T
R2
P
T
'
P
T
P
SP