HEIDENHAIN SW 54843x-03 DIN Programming - Příručka (Stránka 250)

250 Programování podle DIN
4.10 P
římé a kruhové pohyby
Kruhový pohyb G2/G3
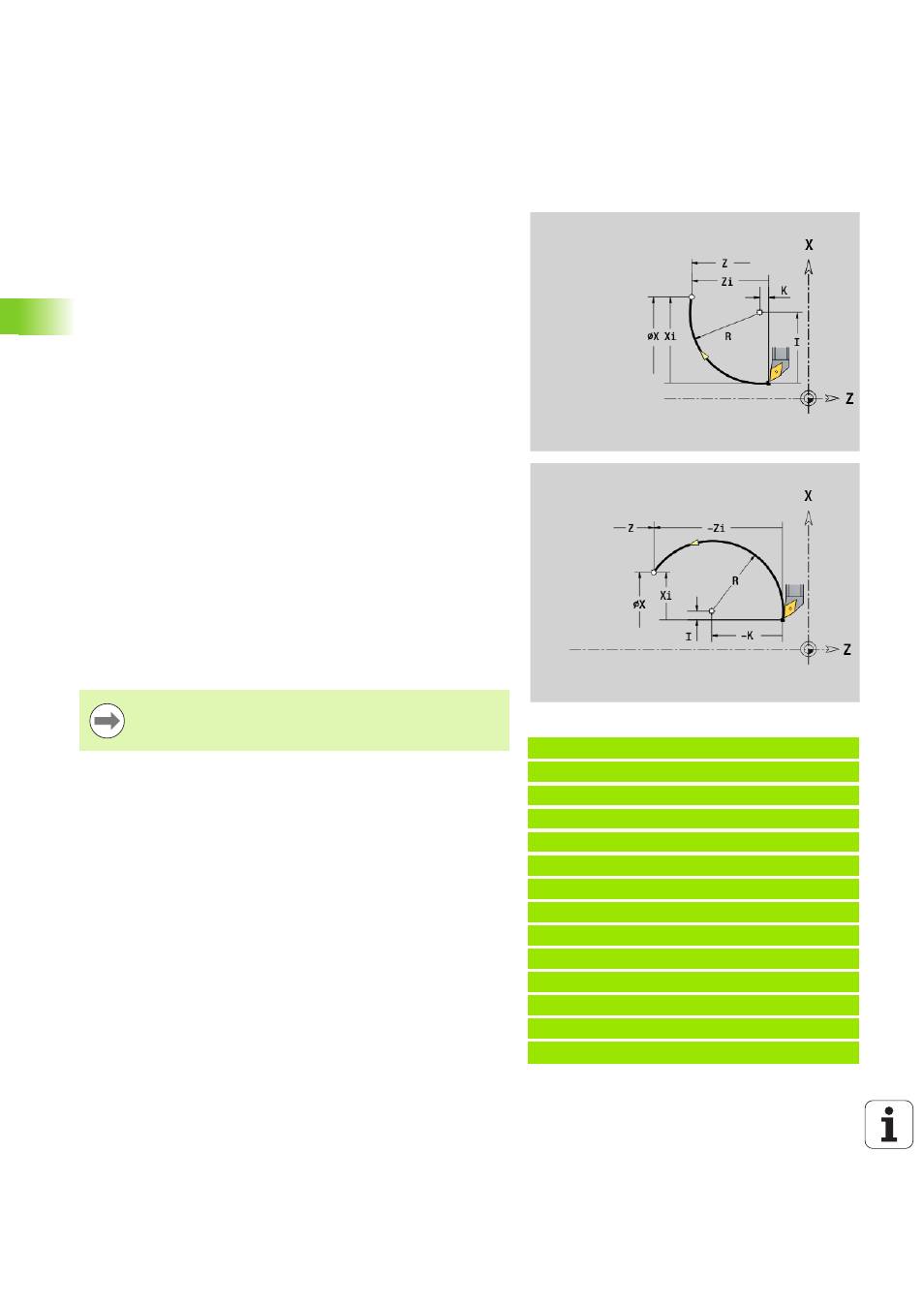
G2 / G3 pojíždí po kruhu posuvem do „Koncového bodu“. Kótování
středu se provádí přírůstkově. Směr otáčení (viz pomocný obrázek):
 G2: ve směru hodinových ručiček
 G3: proti směru hodinových ručiček
Przykład: G2, G3
N1 T3 G95 F0.25 G96 S200 M3
N2 G0 X0 Z2
N3 G42
N4 G1 Z0
N5 G1 X15 B-0.5 E0.05
N6 G1 Z-25 B0
N7 G2 X45 Z-32 R36 B2
N8 G1 A0
N9 G2 X80 Z-80 R20 B5
N10 G1 Z-95 B0
N11 G3 X80 Z-135 R40 B0
N12 G1 Z-140
N13 G1 X82 G40
. . .
Parametry
X
Koncový bod (průměr)
Z Koncový bod
R Rádius (0 < R <= 200 000 mm)
I Střed přírůstkově (vzdálenost výchozí bod – střed; jako rozměr
poloměru)
K Střed přírůstkově (vzdálenost výchozí bod – střed)
Q Průsečík. Koncový bod, pokud oblouk protíná přímku nebo
oblouk kružnice (standardně: 0):
 0: bližší průsečík
 1: vzdálenější průsečík
BR Zkosení / zaoblení. Definuje přechod k dalšímu obrysovému
prvku. Zadáváte-li zkosení/zaoblení, programujte teoretický
koncový bod.
 Bez zadání: Tangenciální přechod
 BR=0: Netangenciální přechod
 BR\>0: Rádius zaoblení
 BR<0: Šířka zkosení
BE Speciální koeficient posuvu pro zkosení/zaoblení (standardně: 1)
Speciální posuv = aktivní posuv * BE (0 < BE <= 1)
Programování X, Z: absolutně, inkrementálně,
samodržně nebo „?“